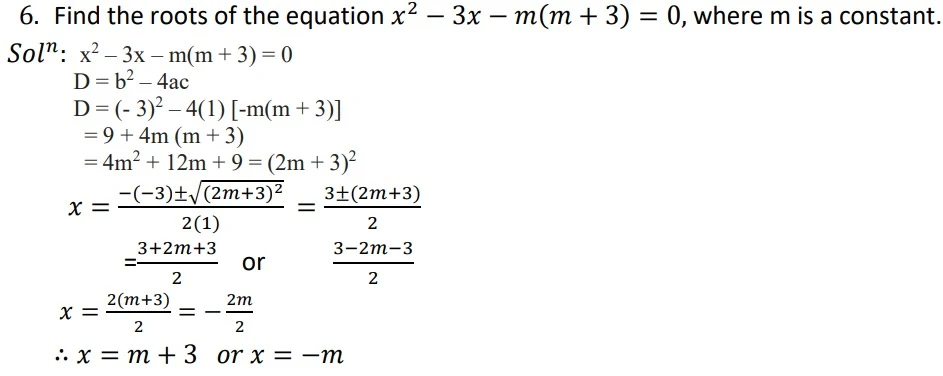Chapter 4. Quadratic Equations CBSE Math Notes

Chapter 4: Quadratic Equations - Class 10

Quadratic Polynomials

⇒ A polynomial of the form a x2 + bx + c, where a, b, and c are real numbers and a ≠ 0, is called a quadratic polynomial.

⇒ The degree of the polynomial is 2.

⇒ A quadratic polynomial of the form a x2 + bx + c, where a ≠ 0 and a, b, and c are real numbers, is called a quadratic equation.

i.e., a x2 + bx + c = 0

  • a is the coefficient of x2
  • b is the coefficient of x
  • c is the constant term

Zero of a Quadratic Polynomial

⇒ A real number α is said to be a zero of quadratic polynomial p(x) = a x2 + bx + c if p(x) = 0.

Example: If p(x) = x2 + 6x + 5, then x = -5 is a zero of the polynomial because it satisfies p(x) = 0.

Root of a Quadratic Equation

⇒ The values of x for which a quadratic equation is satisfied are called the roots of the quadratic equation.

A quadratic equation can have:

  • Two distinct real roots
  • Two equal roots
  • No real roots

Methods to Solve Quadratic Equations

⇒ There are three methods to solve quadratic equations:

  1. Factorisation Method (Splitting the Middle Term)
  2. Completing the Square Method
  3. Quadratic Formula Method (Sridharacharya Formula)

1. Factorisation Method

⇒ In this method, we factorise the quadratic equation into two linear factors and solve for the roots.

Steps:

  1. Factorise the equation using the splitting the middle term method.
  2. Set both factors equal to zero and solve for x.

Example:

For the quadratic equation x2 - 2x - 15 = 0:

(x + 3)(x - 5) = 0
x = -3 or x = 5

The roots are x = {-3, 5}.

2. Completing the Square Method

⇒ This method involves completing the square to solve the quadratic equation.

3. Quadratic Formula Method

Nature of Roots of Quadratic Equation

⇒ The discriminant D helps us determine the nature of the roots:

Example: