Chapter 2: Polynomials
➥A polynomial is an expression in which the power of the variable is a whole number.
Example: −𝑥 + 2𝑥, 𝑥3 + 𝑥2 + 3𝑥 + 4, 𝑥3 + 3, 6, etc.Classification of Polynomials
| 1. Based on Degree | 2. Based on Terms |
|---|---|
| Linear Polynomial (e.g.: 2x + y + 4) | Monomial (e.g.: 3x) |
| Quadratic Polynomial (e.g.: 3x2 - 8x + 9) | Binomial (e.g.: x2 + 3) |
| Cubic Polynomial (e.g.: 4x3 - x2 + 6x + 3) | Trinomial (e.g.: x3 + 2x2 - x) |
Constants and Variables
Constant: Values that do not change (e.g., 3, 4, 10).Variable: Values that can change (e.g., a, b, x, y, z).
Fundamentals
p(x) = a0xn + a1xn-1 + a2xn-2 + ... + an
Where a0, a1, a2, ..., an are constants (Real Numbers); and a0 ≠ 0.
Degree of Polynomial
➥If n = 1, the polynomial is called a linear polynomial.
General form: ax + b, where a ≠ 0
➥If n = 2, the polynomial is called a quadratic polynomial.
General form: ax2 + bx + c, where a ≠ 0
➥If n = 3, the polynomial is called a cubic polynomial.
General form: ax3 + bx2 + cx + d, where a ≠ 0
Zeroes of a Polynomial
➥ The value of x for which p(x) = 0 is called the zero(es) of the polynomial.
➥ A linear polynomial can have at most 1 root.
➥ A quadratic polynomial can have at most 2 roots.
➥ A cubic polynomial can have at most 3 roots.
Relationship between zeroes and coefficient of polynomial:
Division Algorithm for Polynomials
Division Algorithm
If p(x) and g(x) are two polynomials with g(x) ≠ 0, then we can find q(x) and r(x), such that:
p(x) = g(x) × q(x) + r(x)
In simple words: Dividend = Divisor × Quotient + Remainder
Tips
1. The graph of a linear equation is a straight line, while the graph of a quadratic equation is a parabola.
2. The degree of a polynomial is the maximum number of zeroes of the polynomial.
3. If the remainder r(x) = 0, then g(x) is a factor of p(x).
4. To form a quadratic polynomial, if the sum and product of zeroes are given:
P(x) = x² – (sum of zeroes) × x + (product of zeroes)
Graph of a Linear Polynomial
Graph of a Linear Polynomial
The graph of a linear polynomial is a straight line that intersects the x-axis at only one point. Therefore, a linear polynomial has a degree of 1.
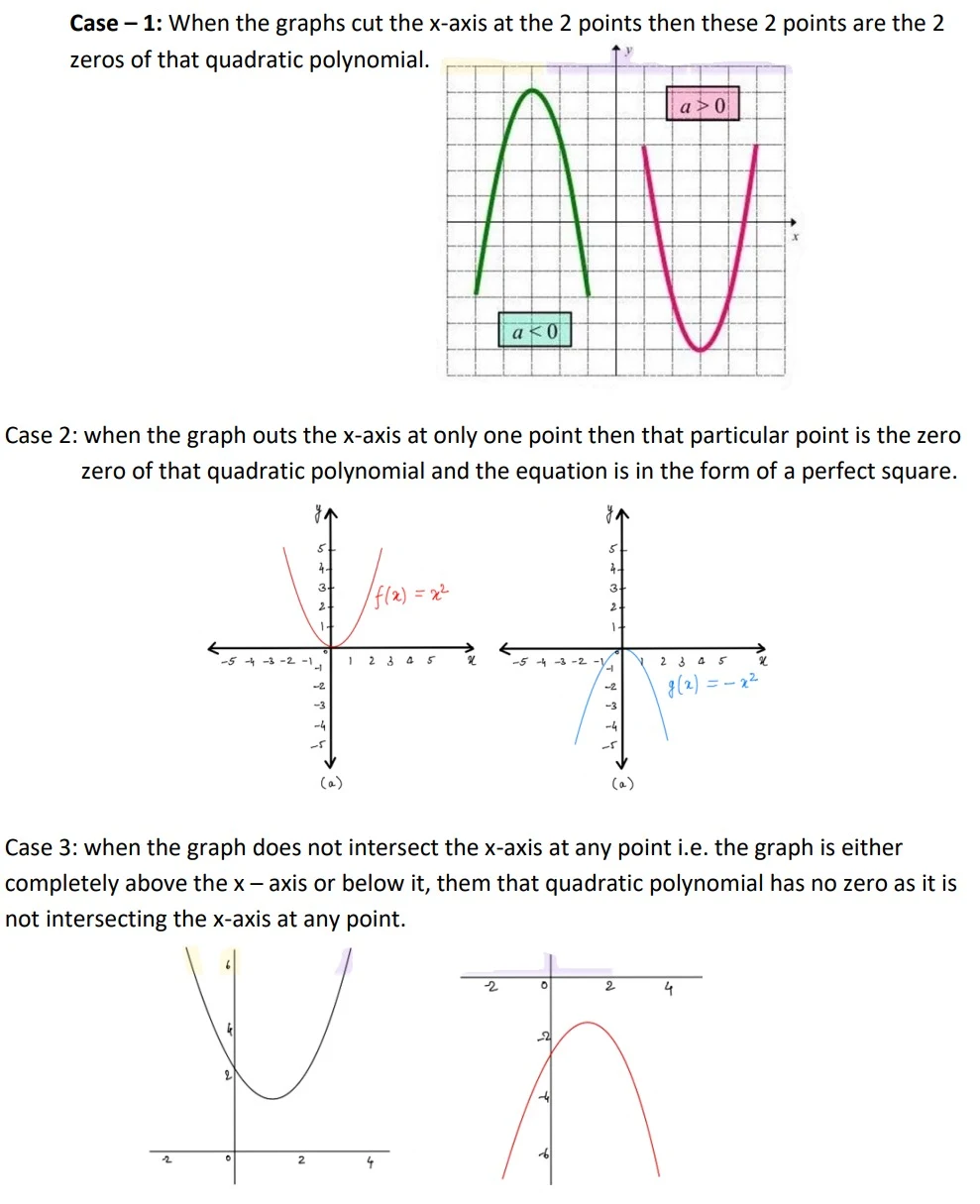
Graph of a Quadratic Polynomial
Graph of a Cubic Polynomial
The graph of a cubic polynomial can intersect the x-axis at most 3 times, meaning it can have up to 3 real zeroes.
Question
Que.Divide the polynomial P(x) by the polynomial g(x). Find the quotient and remainder in each of the following cases.
